Trong thế giới vật lý, vận tốc dao động điều hòa và gia tốc là hai khái niệm cốt lõi giúp chúng ta hiểu sâu sắc về chuyển động tuần hoàn. Chuyển động này, dù thoạt nhìn có vẻ phức tạp, lại xuất hiện phổ biến trong nhiều hiện tượng tự nhiên và ứng dụng kỹ thuật, từ con lắc đồng hồ, lò xo rung động đến các sóng âm thanh và điện từ. Bài viết này sẽ đi sâu vào bản chất, phương trình, đồ thị cũng như mối liên hệ giữa vận tốc và gia tốc trong dao động điều hòa, mang đến cho bạn cái nhìn toàn diện và dễ hiểu nhất.
Hiểu Rõ Về Vận Tốc Trong Dao Động Điều Hòa
Vận tốc là đại lượng đặc trưng cho sự biến đổi nhanh hay chậm của li độ theo thời gian. Trong dao động điều hòa, vận tốc không giữ nguyên một giá trị cố định mà luôn thay đổi, tuân theo một quy luật nhất định.
1. Phương Trình Của Vận Tốc
Khi vật thực hiện dao động điều hòa, li độ của nó được mô tả bằng phương trình (x = Acos(omega t + varphi)). Để tìm phương trình vận tốc, ta lấy đạo hàm của li độ theo thời gian:
(v = frac{dx}{dt} = frac{d}{dt} [Acos(omega t + varphi)])
Kết quả ta thu được là phương trình vận tốc:
(v = – omega Asin (omega t + varphi ))
Từ phương trình này, chúng ta có thể rút ra một số nhận xét quan trọng:
-
Biến thiên tuần hoàn: Vận tốc của vật dao động điều hòa cũng biến thiên tuần hoàn theo quy luật hàm sin (hoặc cosin) với cùng chu kì (T) và tần số góc (omega) như li độ.
-
Quan hệ với li độ: Vận tốc có mối quan hệ chặt chẽ với li độ. Khi li độ cực đại (ở vị trí biên), vận tốc bằng 0. Khi li độ bằng 0 (ở VTCB), vận tốc có độ lớn cực đại.
-
Độ lớn của vận tốc: Ta có thể biểu diễn độ lớn của vận tốc qua li độ bằng cách sử dụng mối liên hệ giữa hàm sin và cosin:
(left| v right| = omega Asqrt {1 – {{cos }^2}(omega t + varphi )} )
Thay (cos (omega t + varphi ) = frac{x}{A}) vào biểu thức trên, ta được:
(v = pm omega sqrt {{A^2} – {x^2}} )
Ý nghĩa của công thức này rất trực quan:
- Khi vật ở Vị trí Cân Bằng (VTCB), tức là (x = 0), độ lớn vận tốc đạt cực đại: (left| v right|_{max} = omega A). Vận tốc có thể dương hoặc âm tùy thuộc vào chiều chuyển động.
- Khi vật ở vị trí biên, tức là (x = pm A), độ lớn vận tốc bằng 0, (v = 0). Điều này hoàn toàn hợp lý vì tại điểm dừng lại trước khi đổi chiều, vận tốc phải bằng không.
2. Đồ Thị Của Vận Tốc
Đồ thị của vận tốc theo thời gian là một đường hình sin (hoặc cosin) lệch pha so với đồ thị li độ. Khi li độ đạt cực đại dương hoặc âm, vận tốc bằng 0. Khi li độ bằng 0, vận tốc đạt cực đại dương hoặc âm. Đồ thị này giúp ta hình dung rõ hơn sự biến thiên của vận tốc trong suốt chu kì dao động.
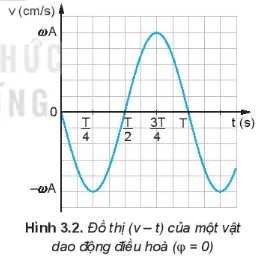 Đồ thị vận tốc trong dao động điều hòa
Đồ thị vận tốc trong dao động điều hòa
Khám Phá Gia Tốc Trong Dao Động Điều Hòa
Gia tốc là đại lượng đặc trưng cho sự biến đổi của vận tốc theo thời gian. Trong dao động điều hòa, gia tốc có những tính chất rất đặc biệt và liên quan mật thiết đến vị trí của vật.
1. Phương Trình Của Gia Tốc
Để tìm phương trình gia tốc, ta lấy đạo hàm của phương trình vận tốc theo thời gian:
(a = frac{dv}{dt} = frac{d}{dt} [- omega Asin(omega t + varphi)])
Kết quả ta thu được là phương trình gia tốc:
(a = – {omega ^2}Acos (omega t + varphi ))
Quan sát phương trình này, ta có thể thấy mối liên hệ sâu sắc giữa gia tốc và li độ:
(a = – {omega ^2}x)
Đây là một đặc điểm quan trọng của dao động điều hòa: gia tốc luôn tỉ lệ thuận với li độ và luôn hướng về vị trí cân bằng (dấu trừ chỉ ra hai đại lượng này luôn ngược chiều nhau).
Các trường hợp đặc biệt của gia tốc:
- Khi vật ở Vị trí Cân Bằng (VTCB), tức là (x = 0), gia tốc bằng 0: (a = 0).
- Khi vật ở vị trí biên, tức là (x = pm A), gia tốc đạt độ lớn cực đại: (left| a right|_{max} = omega ^2 A). Gia tốc có thể là (omega ^2 A) (khi ở biên âm) hoặc (-omega ^2 A) (khi ở biên dương).
2. Đồ Thị Của Gia Tốc
Đồ thị của gia tốc theo thời gian cũng là một đường hình sin (hoặc cosin). Gia tốc sẽ bằng 0 tại VTCB và đạt giá trị cực đại (hoặc cực tiểu) tại các vị trí biên. Điều thú vị là đồ thị gia tốc cùng pha với li độ (nếu li độ được biểu diễn bằng cos) nhưng ngược pha với vận tốc.
 Đồ thị gia tốc trong dao động điều hòa
Đồ thị gia tốc trong dao động điều hòa
Mối Quan Hệ Giữa Vận Tốc, Gia Tốc Và Li Độ
Sự biến thiên của vận tốc, gia tốc và li độ trong vận tốc dao động điều hòa có mối liên hệ tương hỗ chặt chẽ, tạo nên tính chất tuần hoàn đặc trưng.
- Tại VTCB (x=0): Li độ nhỏ nhất, vận tốc có độ lớn cực đại ((left| v right| = omega A)), gia tốc bằng 0 ((a=0)). Vật đang chuyển động nhanh nhất về phía biên đối diện.
- Tại Vị trí Biên ((x=pm A)): Li độ có độ lớn cực đại, vận tốc bằng 0 ((v=0)), gia tốc có độ lớn cực đại ((left| a right| = omega^2 A)). Vật đang tạm dừng lại để đổi chiều chuyển động.
- Giữa VTCB và Biên: Khi vật di chuyển từ VTCB ra biên, li độ tăng dần, vận tốc giảm dần về độ lớn, gia tốc tăng dần về độ lớn và luôn hướng về VTCB. Ngược lại, khi vật di chuyển từ biên về VTCB, li độ giảm dần, vận tốc tăng dần về độ lớn, gia tốc giảm dần về độ lớn và vẫn hướng về VTCB.
Biểu đồ Vận tốc – Li độ
Ngoài đồ thị theo thời gian, ta còn có thể xét mối quan hệ giữa vận tốc và li độ bằng biểu thức (v^2 + (omega x)^2 = (omega A)^2). Biểu thức này cho thấy mối quan hệ dạng elip (hoặc hypebol tùy cách biểu diễn) giữa vận tốc và li độ, khẳng định lại rằng khi (x=pm A) thì (v=0), và khi (x=0) thì (left| v right| = omega A).
Lưu Ý Quan Trọng Khi Nghiên Cứu Vận Tốc, Gia Tốc
Khi làm việc với các bài toán về dao động điều hòa, đặc biệt là các dạng vận tốc dao động điều hòa, người học cần lưu ý một số điểm sau để tránh sai sót:
- Dấu của Vận Tốc và Gia Tốc: Luôn chú ý đến dấu của vận tốc và gia tốc. Dấu của vận tốc cho biết chiều chuyển động, còn dấu của gia tốc cho biết hướng tác dụng của lực phục hồi.
- Độ Lớn Cực Đại: Phân biệt rõ khi nào vận tốc và gia tốc đạt độ lớn cực đại (tại VTCB cho vận tốc, tại biên cho gia tốc) và khi nào chúng bằng 0 (tại biên cho vận tốc, tại VTCB cho gia tốc).
- Pha Dao Động: Hiểu rõ mối quan hệ về pha giữa li độ, vận tốc và gia tốc. Vận tốc trễ pha (frac{pi}{2}) so với li độ, còn gia tốc ngược pha với li độ.
- Ứng Dụng Thực Tế: Nhận diện các hiện tượng trong cuộc sống có thể mô tả bằng dao động điều hòa để hiểu sâu hơn về các khái niệm vật lý. Ví dụ, chuyển động của một quả bóng trên lò xo, sự rung động của dây đàn guitar khi gảy, hay thậm chí là chuyển động của các phân tử trong vật chất ở một mức độ nào đó.
Sơ Đồ Tư Duy Tổng Quan
Để củng cố kiến thức, sơ đồ tư duy dưới đây tóm lược các ý chính về Vận tốc và Gia tốc trong Dao động Điều hòa:
 Sơ đồ tư duy về “Vận tốc, gia tốc trong dao động điều hòa”
Sơ đồ tư duy về “Vận tốc, gia tốc trong dao động điều hòa”
Hiểu rõ về vận tốc và gia tốc là bước đệm quan trọng để chinh phục các dạng bài tập phức tạp hơn và áp dụng kiến thức vật lý vào giải thích thế giới xung quanh.
Ngày chỉnh sửa 07/01/2026 by Anh Ngân
